Time for a little physics, then:
 BB Characteristics:
Radii
BB Characteristics:
Radii
BBr1: 5.98mm = 0.00598m
BBr2: 5.98mm = 0.00598m
Masses
BBm1: .20g = .002kg
BBm2: .25g = .0025kg
Velocity
BBv1: 400 f/s or 121.92 m/s
BBv2: 358 f/s or 109.12 m/s
Coefficient of drag for a sphere is .47
We'll just use air density as a unit of 1kg/m^3, for simplicity
Calculating Cross-Sectional Area:
BBsa1: pi*r^2 = pi*.00598^2 =
0.000112m^2
BBsa2: pi*r^2 = pi*.00598^2 =
0.000112m^2
Calculating Drag Force:
Where csa = cross-sectional area, rho = air density, cd = coefficient of drag.
BBdf1: 0.5*v^2*csa*rho*cd = 0.5*121.92^2*0.000112*1*0.47 =
.391N
BBdf2: 0.5*v^2*csa*rho*cd = 0.5*109.12^2*0.000112*1*0.47 =
.313N
Calculating Deceleration of the BB
F=ma, where F = force, m = mass, and a = acceleration. Rewrite as a=F/m.
These are negative values because it's acceleration in the negative direction:
BBa1: a = F/m = .391/.002 =
-195.5 m/s^2
BBa2: a = F/m = .313/.0025 =
-125.2 m/2^2
This is deceleration in the plane
opposite the velocity vector, since all objects decelerate (or accelerate downwards) at a rate of 9.8 m/s^2 due to gravity (the y-plane).
The difference seems somewhat negligible in distances as small as 200 feet (60.96 meters)...
Now, projectile motion with the inclusion of air resistance delves into differential equations, and while I've been through the course, I don't feel like diving into it at midnight on a Monday night. My classes don't start for another month or so and I've already done much too much math tonight. So, I downloaded a program that would run it for me, because today is the future and we can do stuff like this. Below are the results (1.7m is the average height of a man, assuming firing at a target at an equal altitude):
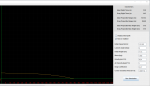
.20:
![]()
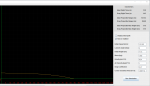
.25:
![]()
The .20 covered 54.36 meters in .65 seconds, giving it an average velocity of: 83.63 m/s or 274.38 f/s.
The .25 covered 52.00 meters in .63 seconds, giving it an average velocity of: 82.54 m/s or 270.80 f/s.
At this distance (~175 feet), given the velocities from that website (400fps at .20 = 358fps at .25), the .20 wins for time on target.
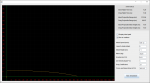
I'm not satisfied:
![]()
I messed with the initial height until I had both the BBs landing about ~90 meters away from the starting point, which is right around the 300 foot mark, where all of these pro-DMR-ers claim to be reaching out to (and it is possible). Of course, this program can't simulate hop-up, but this is just a BB weight battle, not including hop-up effects.
.20:
![]()
.25:
![]()
The .20 covered 89.68 meters in 1.42 seconds, giving it an average velocity of: 63.15 m/s or 207.19 f/s.
The .25 covered 89.97 meters in 1.38 seconds, giving it an average velocity of: 65.20 m/s or 213.91 f/s.
The .25 starts to overtake the .20 at distances around ~70-80 meters, I believe. I could find the exact number by calculating the intercept, but no thanks.
*FUN FACT* Without air resistance, we'd be able to shoot about 25% further, at the distances we usually play at.
TLDR: The difference in the velocity of the round doesn't matter nearly as much as we all think it might, since the lighter rounds are affected by drag more than the heavier rounds. You are better off using a heavier round, since on top of a very, very, very, very small drawback of time on target (that actually becomes better than lighter BBs, the further you are shooting), you get better accuracy and much better wind resistance.
Use heavier BBs.
Enough physics, calculus, and math in general for Spaceman tonight.